Unreal Engine - Render First-Person Meshes with a Separate FOV (Viewmodel/First-Person/Weapon FOV) // Sahil Dhanju's Blog

Throughout the development of a first-person game, designers tweak and iterate the camera’s FOV based on gameplay needs. However, animators will often animate at a specific FOV in their animation software. Playing an animation animated at a FOV of 60 will look very different at a FOV of 120. So if designers are constantly changing the FOV of the game, it’s quite a hassle for animators to constantly adjust their animations every time there is a tweak.

Because of this, First-person games often separate “FOV” into two separate FOVs:

World Field of View - the FOV of the player’s camera
Viewmodel FOV - the FOV used to render the first-person meshes (arms, weapon, etc.) This FOV has different names so you may have seen a different term for this.

Below I’ll show how to render the player’s first person meshes using a different FOV in Unreal Engine using C++ (sorry, this wouldn’t work with only Blueprints). The strategy used can be applied generically to any engine. The article assumes you have basic knowledge about how an object gets rendered on screen. If you aren’t familiar with this here are some great resources you can read if you’re wanting to understand this implementation.

if aren’t too interested in how it works, feel free to scroll to the bottom to take a look at the code.

The Idea

UPrimitiveComponent is the base component for anything renderable in Unreal. All Meshes, Skeletons, Particles, Lights, etc. derive from UPrimitiveComponent. Within it, there is this function

    /** 
     * Returns the matrix that should be used to render this component. 
     * Allows component class to perform graphical distortion to the component not supported by an FTransform 
     */
    virtual FMatrix GetRenderMatrix() const;

Unreal calls this function on every PrimitiveComponent in the scene ever frame to get the Model matrix of the component. The model matrix is used to eventually render this component on screen.

This is our hook into Unreal’s rendering pipeline. We can freely override this function and return whatever matrix we want.

Our goal will be to calculate a model matrix that ends up having the effect of rendering this component at our specified Viewmodel FOV.

The Math

The calculation to render an object with a camera that has the World FOV is

$${M} \cdot {V} \cdot {P_{world}} = T $$

where

$M$ - The model matrix of the object
$V$ - The view matrix of the camera
$P_{world}$ - The projection matrix with a World FOV
$T$ - The resulting transform of the object in NDC space.

$M$ is what is returned by GetRenderMatrix, so this is the matrix we can adjust to get us to an object rendered with the viewmodel FOV. Let’s call this adjusted model matrix $M_{adj}$. For an object rendered at the viewmodel FOV, the calculation would be

$${M} \cdot {V} \cdot {P_{viewmodel}} = T $$

Where $P_{viewmodel}$ is the projection matrix with the viewmodel FOV. The left hand side of this equation is what our desired calculation should be. So we can form this expression

$${M_{adj}} \cdot {V} \cdot {P_{world}} = {M} \cdot {V} \cdot {P_{viewmodel}}$$

We need to figure out $M_{adj}$ such that after passing through the rendering pipeline, it yields the right side of the expression.

One observation here is if $M_{adj}$ somehow could cancel the ${P_{world}}$ multiplication, then we could potentially set $M_{adj}$ to be the right-hand side of the expression. However to cancel out ${P_{world}}$ we need to cancel out $V$ first. We can do this by first multiplying by $V^{-1}$ on the right- hand side, and then by ${P^{-1}_{world}}$.

So we get this expression

$$( {M_{adj’}} \cdot {P^{-1}_{world}} \cdot {V^{-1}}) \cdot {V} \cdot {P_{world}} = {M} \cdot {V} \cdot {P_{viewmodel}}$$

Where ${M_{adj}} = {M_{adj’}} \cdot {P^{-1}_{world}} \cdot {V^{-1}}$

If we do the multiplication with ${V^{-1}} \cdot {V}$, they cancel, so we’re left with

$${M_{adj’}} \cdot {P^{-1}_{world}} \cdot {P_{world}} = {M} \cdot {V} \cdot {P_{viewmodel}}$$

And $P_{world}^{-1} \cdot {P_{world}}$ cancels again, so we’re left with

$${M_{adj’}} = {M} \cdot {V} \cdot {P_{viewmodel}}$$

meaning

$${M_{adj}} = {M} \cdot {V} \cdot {P_{viewmodel}} \cdot {P^{-1}_{world}} \cdot {V^{-1}}$$

And we’re done! This is the matrix we need to calculate to be returned by GetRenderMatrix()

As an optimization, I noticed that ${P_{viewmodel}}$ and ${P^{-1}_{world}}$ can be combined into a straightforward matrix that only uses the ratio of the world FOV to the viewmodel FOV. This matrix, which I’ll call $P_{adj}$, looks like

$$ P_{adj} = \begin{bmatrix}\frac{world}{viewmodel}\ & 0 & 0 & 0\\ 0 & \frac{world}{viewmodel} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{bmatrix}$$

You can try deriving this yourself if you’re interested :)

The final calculation for $M_{adj}$ is

$${M_{adj}} = {M} \cdot {V} \cdot {P_{adj}} \cdot {V^{-1}}$$

The Code

In C++, I make a new class called UViewmodelSkeletalMeshComponent which extends USkeletalMeshComponent. I’m only implementing this feature for skeletal meshes at the moment but you can very easily implement this for static meshes or any other primitive component.


// ViewmodelSkeletalMeshComponent.h

UCLASS(BlueprintType, meta = (BlueprintSpawnableComponent))
class MYPROJECT_API UViewmodelSkeletalMeshComponent : public USkeletalMeshComponent
{
    GENERATED_BODY()

public:
    UPROPERTY(EditAnywhere)
    float DesiredViewmodelFOV = 70.0f;

protected:
    virtual void BeginPlay() override;

    virtual FMatrix GetRenderMatrix() const override;

private:
    UPROPERTY()
    APlayerController* PlayerController;

    UPROPERTY()
    APlayerCameraManager* PlayerCameraManager;
};

DesiredViewmodelFOV will be where the value of the viewmodel FOV is set. I also have private references to the PlayerController and PlayerCameraManager since we’ll need this calculating the View matrix.

In BeginPlay, we want to assign references to the PlayerController and PlayerCameraManager

void UViewmodelSkeletalMeshComponent::BeginPlay()
{
    Super::BeginPlay();

    PlayerController = UGameplayStatics::GetPlayerController(this, 0);

    if (PlayerController != nullptr)
    {
        PlayerCameraManager = PlayerController->PlayerCameraManager;
    }
}

Now for GetRenderMatrix - if we start by getting values from the PlayerController and PlayerCameraManager to create the view matrix and $P_{adj}$. In this case it would be

The view origin - where the player’s camera is in the world.
The view rotation - which way the player’s camera is rotating.
The camera’s FOV - the FOV of the player’s camera.

FMatrix UViewmodelSkeletalMeshComponent::GetRenderMatrix() const
{
    // If our references are invalid, don't try to continue with our calculation.
    if (PlayerController == nullptr || PlayerCameraManager == nullptr)
    {
        return Super::GetRenderMatrix();
    }

    const float WorldFOV = PlayerCameraManager->GetFOVAngle();
    const float ViewmodelFOV = DesiredViewmodelFOV;

    FVector ViewOrigin;
    FRotator ViewRotation;
    PlayerController->GetPlayerViewPoint(ViewOrigin, ViewRotation);

    // ...

}

Let’s start with calculating $P_{adj}$. The projection matrix actually uses half the FOV angle in its calculations. Additionally, it expects the angle to be in radians.

FMatrix UViewmodelSkeletalMeshComponent::GetRenderMatrix() const
{
    // ...

    const float WorldHalfFOVRadians = FMath::DegreesToRadians(FMath::Max(0.001f, WorldFOV)) / 2.0f;
    const float DesiredHalfFOVRadians = FMath::DegreesToRadians(FMath::Max(0.001f, ViewmodelFOV)) / 2.0f;
    const float FOVRatio = WorldHalfFOVRadians / DesiredHalfFOVRadians;

    const FMatrix PerspectiveAdjustmentMatrix = FMatrix(
        FPlane(FOVRatio, 0, 0, 0),
        FPlane(0, FOVRatio, 0, 0),
        FPlane(0, 0, 1, 0),
        FPlane(0, 0, 0, 1));
    
    // ...
}

Now for the View Matrix. You can learn more about calculating view matrices here. Essentially all we need to do is put together the ViewOrigin and ViewRotation into a single transform matrix.


FMatrix UViewmodelSkeletalMeshComponent::GetRenderMatrix() const
{
    // ...

    // Create our Rotation Matrix based on the Camera.
    FMatrix ViewRotationMatrix = FInverseRotationMatrix(ViewRotation) * FMatrix(
        FPlane(0, 0, 1, 0),
        FPlane(1, 0, 0, 0),
        FPlane(0, 1, 0, 0),
        FPlane(0, 0, 0, 1));

    // If the Rotation Matrix is not at the origin, add the translation to the 
    // ViewOrigin and then remove it from the Rotation Matrix.
    if (!ViewRotationMatrix.GetOrigin().IsNearlyZero(0.0f))
    {
        ViewOrigin += ViewRotationMatrix.InverseTransformPosition(FVector::ZeroVector);
        ViewRotationMatrix = ViewRotationMatrix.RemoveTranslation();
    }

    const FMatrix ViewMatrix = FTranslationMatrix(-ViewOrigin) * ViewRotationMatrix;

    const FMatrix InverseViewMatrix = FTranslationMatrix(-ViewMatrix.GetOrigin()) * ViewMatrix.RemoveTranslation().GetTransposed();
    
    // ...
}

Now all we need to do is the full calculation I showed above and we’re done!

FMatrix UViewmodelSkeletalMeshComponent::GetRenderMatrix() const
{
    // ...

    const FMatrix AdjustedRenderMatrix = GetComponentToWorld().ToMatrixWithScale() * ViewMatrix * PerspectiveAdjustmentMatrix * InverseViewMatrix;

    return AdjustedRenderMatrix;
}

You can view the full source code here

Results

World FOV at 80

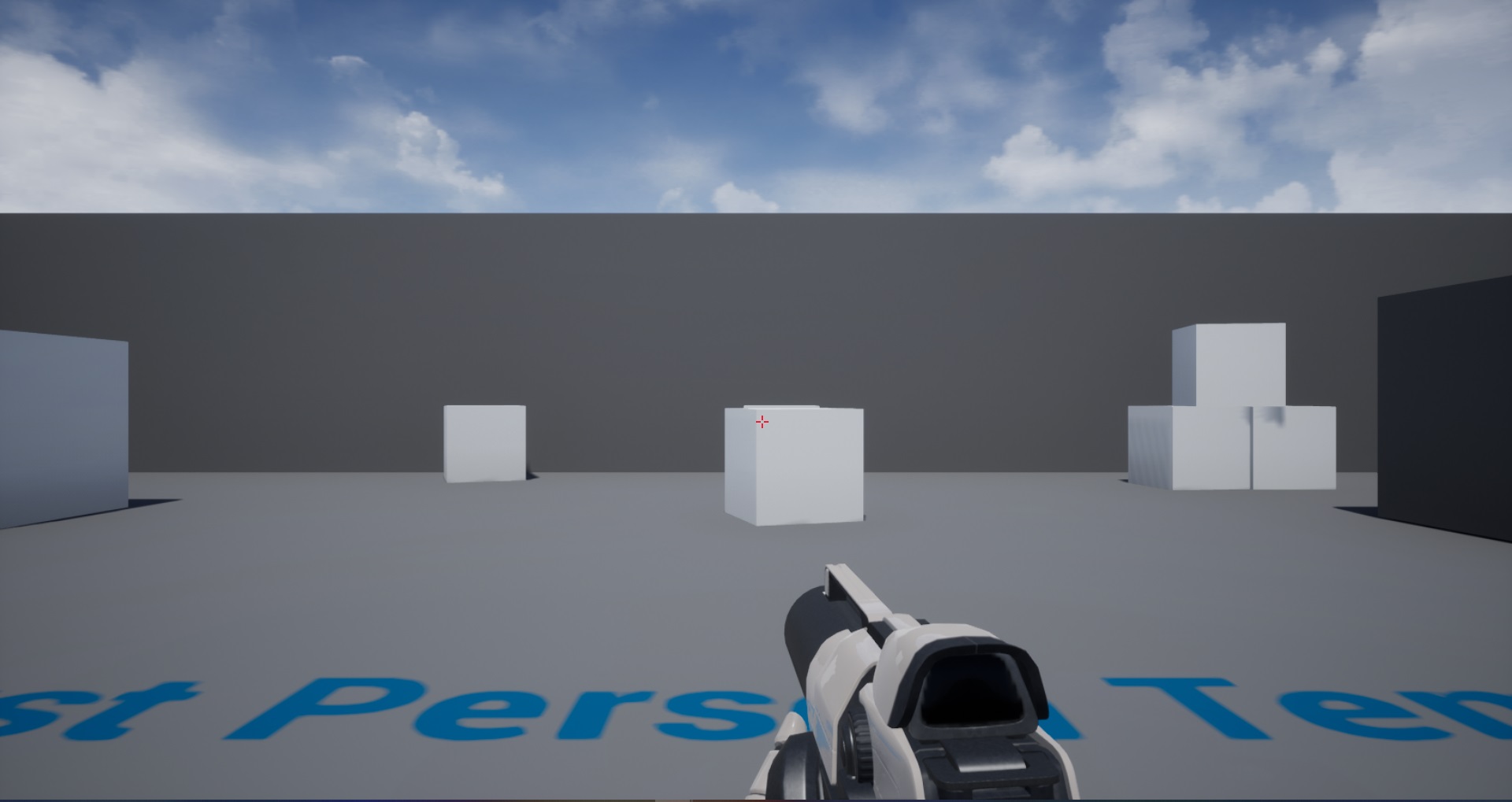
World FOV at 120

World FOV at 120 with Viewmodel FOV at 80

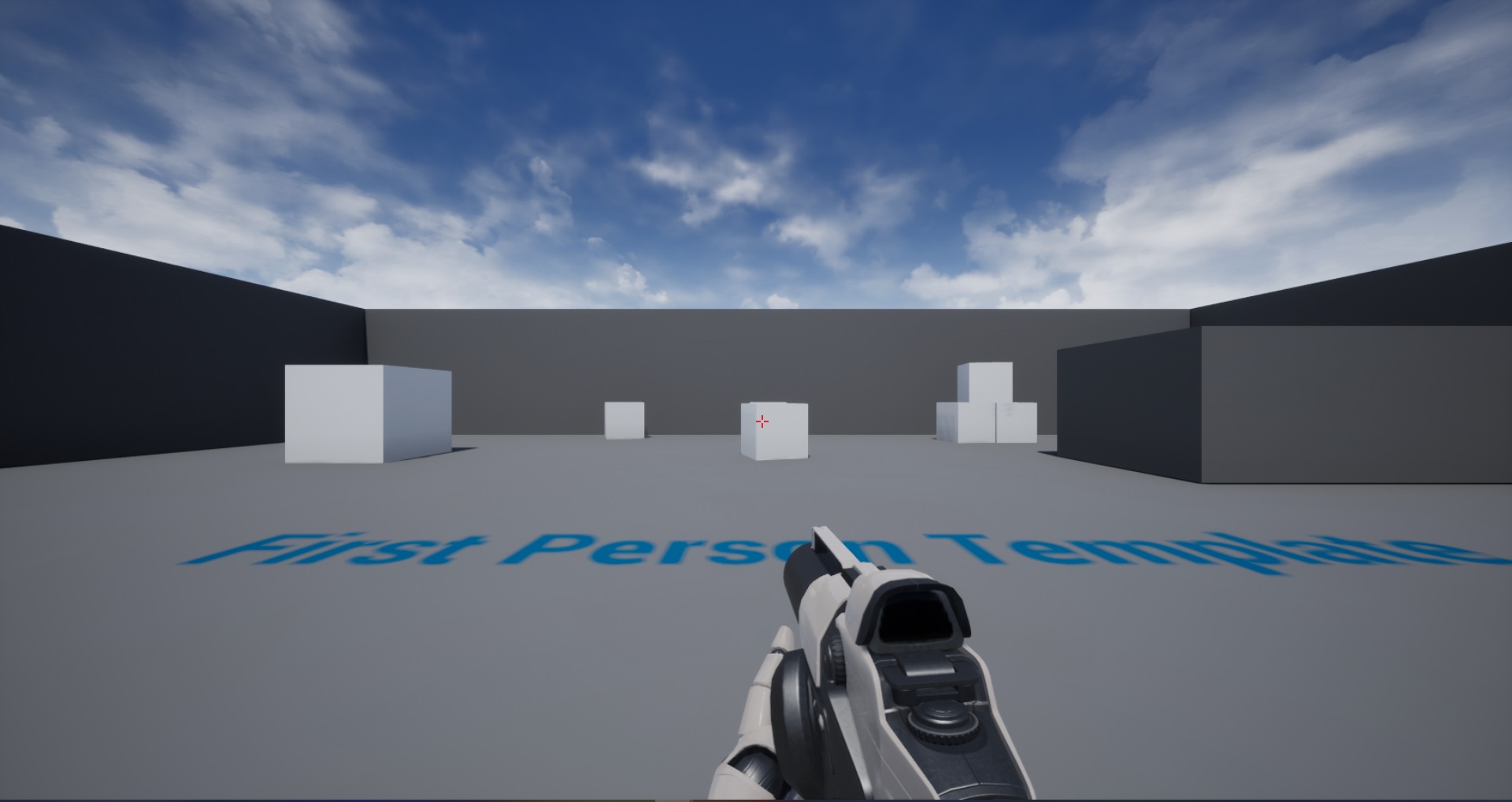
World FOV at 120 with Viewmodel FOV at 60

As you can see, it’s not exact. The Viewmodel FOV of 60 better matches the World FOV at 80 than the Viewmodel FOV at 80. Depending on your use case this might be fine. Two reasons for this can be.

Our desired aspect ratio was never taken into account.
FOV scaling wasn’t taken into account.

This project shows how to convert your desired viewmodel FOV into a Hor+ FOV, which can be scaled more accurately. Ultimately you might need to tweak the actual viewmodel FOV value but you should still be able to achieve the desired look.

Other notes

If you attach anything to your first-person viewmodel, weapon attachments, particle effects, etc., you’ll need to make sure those are also scaled in the same way otherwise they will look misaligned.
In most first-person games, the viewmodel is rendered with a separate render pass so it always appears on top of world geometry. This is separate to what this article has presented and can be done in conjunction.
There are also other ways to achieve the same effect, such as this plugin or using a panini project.
- As for the plugin, in my personal experience it can cause issues with geometry inside of the weapon clipping outside of the weapon depending on your desired FOV so I wouldn’t recommend it.